Générateur de mot de passe Diceware
Générer des mots de passe à haute entropie en toute simplicité!
Essayer un autre navigateur. Sinon, utiliser cette méthode à vos propres risques.
A propos
Diceware
Les mots de passe faibles sont un gros défaut dans la sécurité informatique en raison d'un manque d'«entropie» ou d'aléatoire. Pire encore, si les mots de passe sont réutilisés entre les services, ce qui augmente le risque de sécurité.
Le fait est, les humains ont du mal à se rappeler des combinaisons de lettres et de chiffres aléatoires, mais se souviennent plus facilement d'une phrases contenant des mots. Voilà où Diceware intervient.
Cette application web Diceware est basée sur la proposition http://world.std.com/~reinhold/diceware.html Les dés virtuels au nombre de 5 sont jetés de 2 à 8 fois selon votre choix (choisir au minimum 4), et chaque nombre de 5 chiffres est utilisé comme index dans une table de mots. 4 jets de dés vous donne 4 mots aléatoires de langue française , plus faciles à mémoriser pour un être humain, avec une haute entropie ce qui les rend difficiles à craquer.
Qu’est-ce que l’entropie ?
L’entropie est un concept emprunté à la théorie de l’information. Dans le contexte des mots de passe, l’entropie peut être résumée comme suit : combien de tentatives seraient nécessaires pour deviner un mot de passe par force brute ?
Dans Specops Password Auditor, nous calculons l’entropie des mots de passe de vos politiques de mot de passe avec cette formule :
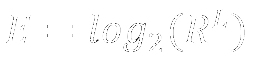
Regardons ce qu’il y a dans cette formule.
Pour calculer l’entropie, nous devons commencer par ces deux mesures
L – La longueur requise du mot de passe
R – La liste de caractères requise
Par exemple, si un mot de passe ne doit contenir que des lettres minuscules, R = 26. Si le mot de passe doit contenir des minuscules, des majuscules et des chiffres, R = 62 (26 + 26 + 10)
L’ensemble des possibilités de mots de passe pour un mot de passe, ou “password space” en anglais, peut alors être calculé comme RL. L’espace de mot de passe est une mesure du nombre total de mots de passe possibles qui peuvent être créés en utilisant une certaine valeur pour L et R. Comme vous pouvez l’imaginer, il s’agit d’un très grand nombre. Par exemple, avec L = 10 et R = 62, l‘espace des mots de passe est de 839 299 365 868 340 224. Comme de telles échelles de nombres sont un peu difficiles à manier, l’entropie est définie comme le logarithme binaire, log2 , de cette valeur. Le logarithme binaire peut également être lu comme le nombre de bits nécessaires pour exprimer le nombre. Cela conduit à la formule complète de l’entropie (E) : E = log2(RL).
Dans l’exemple ci-dessus avec L = 10 et R = 62, l’entropie s’élève à ≈ 60.